Flame in high-velocity flow streams is only stabilized in a certain condition. Determining the range of flame stabilized conditions is an important issue in practical combustion applications. Flame stabilization has been one of the challenging subjects in premixed combustion systems under highly turbulent conditions, such as gas turbine engines and propulsion devices. A bluff-body, known as a flame holder, has been employed as one of flame stabilization schemes, including backward-facing step and swirling flow. While the bluff-body has an advantage of improving flame stability by creating a recirculation zone behind the body, the bluff-body itself also causes instability into the anchored flames. Therefore, understanding the physical mechanisms of combustion stability behind the bluff-body, such as where the flame is stable or extinguishing and the unstable flame dynamics behind the bluff-body, is necessary to predict the combustion stability under wide operating conditions.
Two-dimensional direct numerical simulations are conducted to investigate the dynamics of lean premixed flames stabilized on a mesoscale bluff-body in hydrogen-air and syngas-air mixtures. This study is conducted by direct numerical simulations that solve fully compressible multi-species reacting Navier-Stokes equations with high order explicit discretization in space and explicit integration in time with detailed chemical kinetics. Non-reflecting characteristic boundary conditions are applied to the inflow and outflow boundaries. A square-shape bluff-body is modeled as a union of logical MPI blocks.
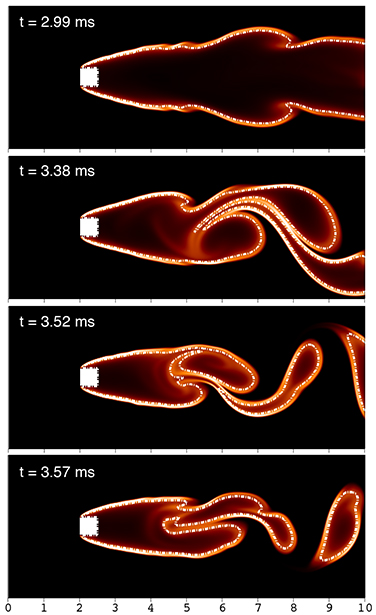
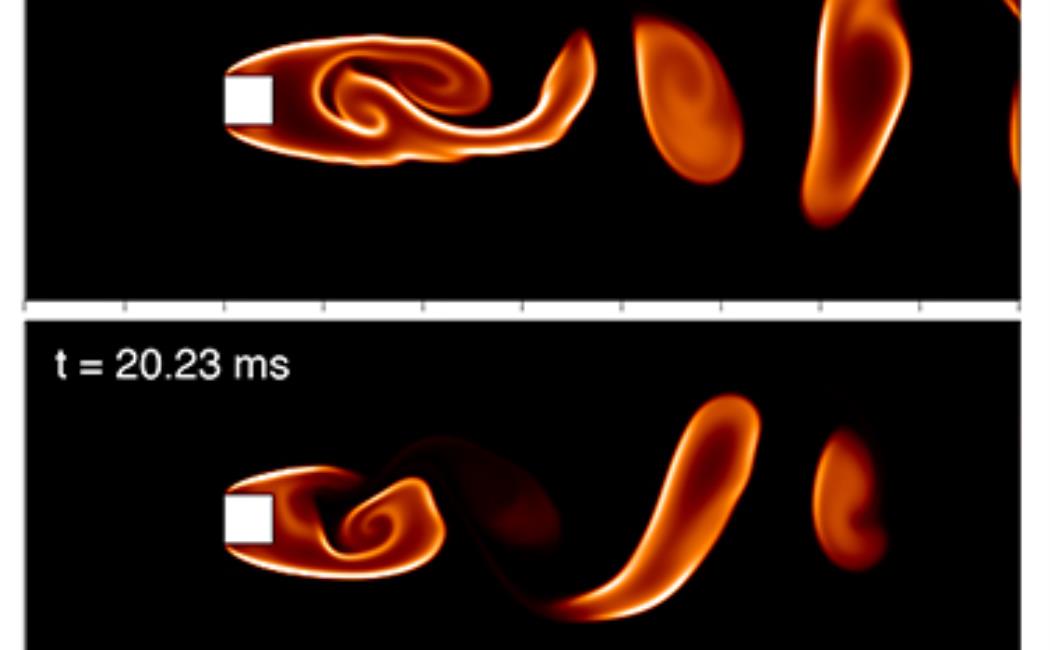
Overall flame dynamics are observed by ramping up the inflow velocity until blow-off occurs. Five distinct flame instabilities are observed such as steadily stable, mild fluctuation, symmetric vortex-shedding, asymmetric vortex-shedding, and vortex street from the low inflow velocity to blow-off limit.