Motivation and Objectives
Adaptive mesh refinement (AMR) can reduce the computational cost significantly, while maintaining the capability to capture flow features at different scales. We develop solvers for compressible multi-species reactive Navier-Stokes equations based on finite-volume methods, with AMR capability.
Approach
by level0set functiuons is implemented. For reacting flows with detailed chemistry, advanced libraries for thermodynamics, transport, and chemical kinetics are implemented with full compatibility in both multi-core and many-core architectures. Higher order finite volume methods allow accurate predictions of the formation and propagation of nonlinear waves.
Highlights of Results
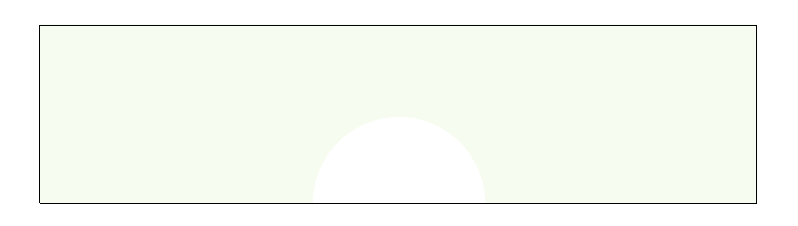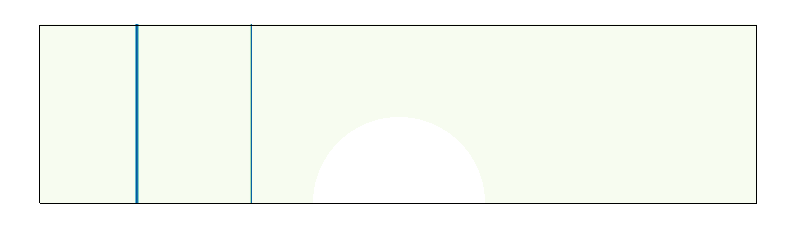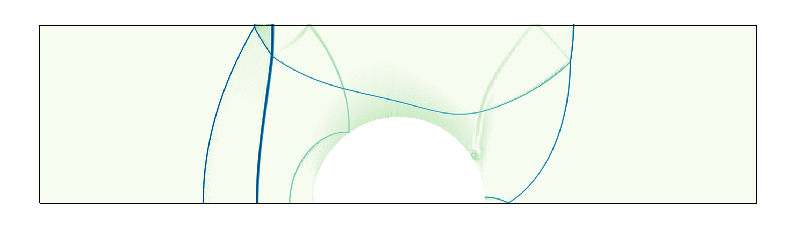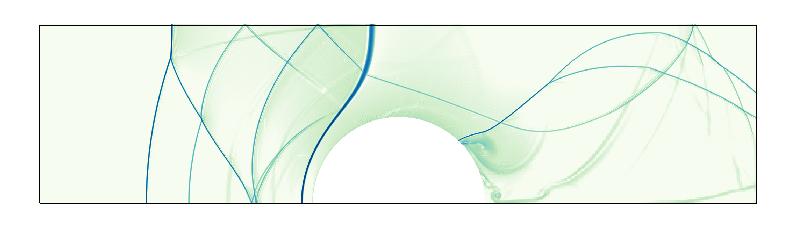
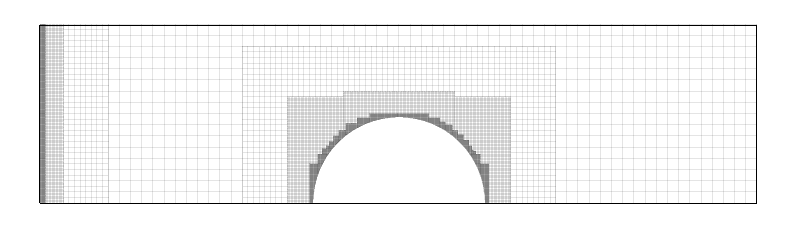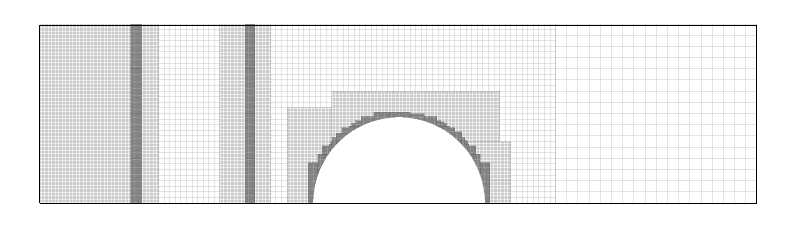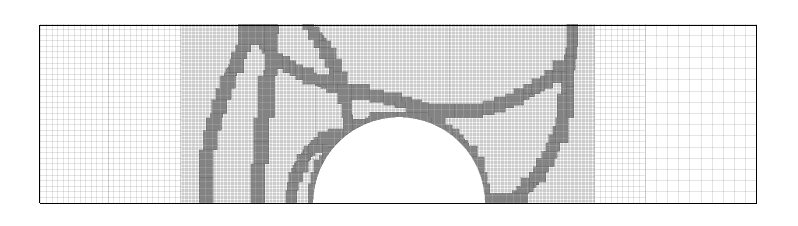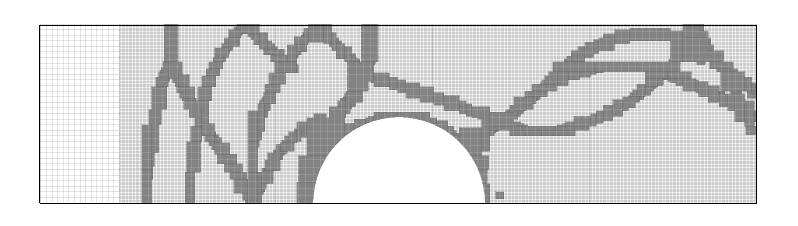
A two-dimensional shock-tube problem (equivalent to Sod’s test) with a cylindrical geometry demonstrates current level-set/ghost-cell method. The evolution of the density (top), pseudo-Schlieren (middle), and the corresponding mesh refinement (bottom) are shown.